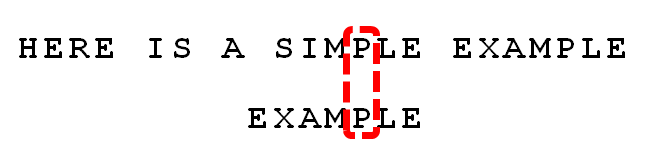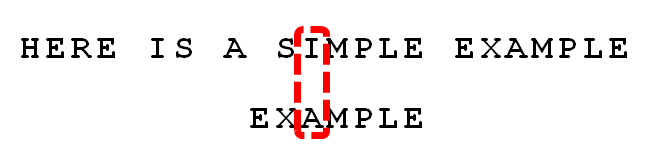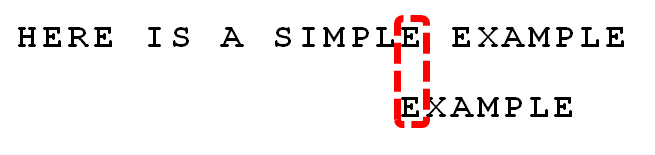为了方便,这里匹配算法只使用字符串处理问题来进行说明(当然,这也可以用于其他序列问题的匹配),而且,匹配算法不同于匹配树,匹配算法一般只用于主串(匹配串)对模式串(不作用于模式串序列)的匹配。
1. 朴素的匹配算法(Naive Algorithm)
实现代码传送门
1.1. 基本思想
朴素算法即暴力匹配算法。其算法思想非常简单。
首先将主串和模式串左对齐;然后将两者从左向右一一进行比较,如果不成功则模式串向右移动一个单位,重复上述比较的步骤,直到匹配成功为止。
例如,出现下面失配情况时
则回溯主串,从下一位开始重新开始匹配
1.2. 优缺点
朴素算法优点是不需要对模式串进行预处理,故预处理的时间复杂度为0
但缺点缺十分明显,该算法对主串进行重复地遍历,匹配的最坏的时间复杂度为 \(O((n-m+1)*m)\) ,其中,\(n\)为主串的长度,\(m\)为模式串的长度。明显的,该算法的效率太低了。
故目前主流的优化算法一般对模式串进行预处理,减少对主串遍历,以提高匹配效率。
2. KMP算法(Knuth-Morris-Pratt Algorithm)
实现代码传送门
2.1. 算法思想
对于主串已经遍历过的部分内容,成为我们已知的先验知识。对于已有的知识,我们不需要再去回溯主串重新遍历一遍。怎样利用已有的先验知识呢?对此,我们需要引入最大公共元素长度。最大公共元素长度即最长相同的前缀和后缀,例如,ABCDAB 的最大公共元素为 AB,长度为2
失配处理
例如,对于给定的主串T BBC ABCDAB ABCDABCDABDE,以及模式串P ABCDABD,当出现下面失配情况时
截取失配片段 t=T[4:10]=P[0:6]=ABCDAB 进行分析
对于 t[1:4]=BCD ,以这些元素开始匹配一定会失配,因为以这些元素作为开头的序列一定不是t的前缀序列,所以这些元素可以直接跳过。
对于 t[4:6]=AB,可以看出这个元素序列是t的前缀序列,故从 t[4] 开始匹配有可能匹配成功。但是,事实上我们并不需要真的回溯到 t[4] ,因为已知 t[4:6]=P[0:2]=AB 已经匹配成功,所以只需从 T[10] 以及 P[2] 开始比较即可(即将P往右挪至 T[8] 位置,使得P和T的 AB 元素重合),如下图所示
综上可以发现,我们是直接从主串中失配的位置继续往后进行匹配,不需要回溯到主串中任何已经匹配过的位置。
特别地,应该可以注意到,失配后,P重新开始时的下标即为t的最大公共元素长度。自然地,我们需要一个保存每个失配片段的最大公共元素长度的数组 next,这个也是KMP算法的重点
next数组的获取
next 数组的获取其实是字符串的自匹配问题,即以模式串为模式串的主串,同时以模式串的前缀为模式串的模式串。
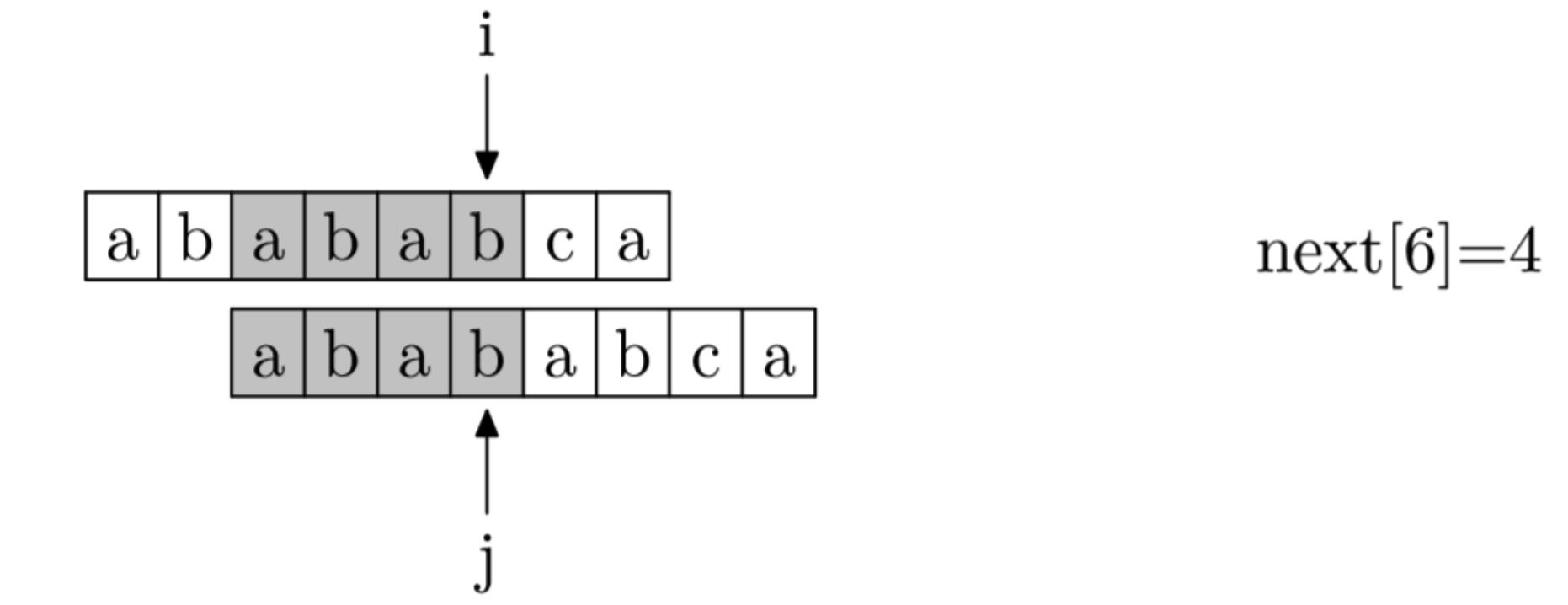
具体来说,复制一条模式串,上下对齐放置,上面作为主串,下面作为模式串。首先对模式串往右挪一位,开始匹配。 在任一位置,如果对应字符相同,则主串当前位置的next值就是模式串当前位置的下标,具体如下图所示
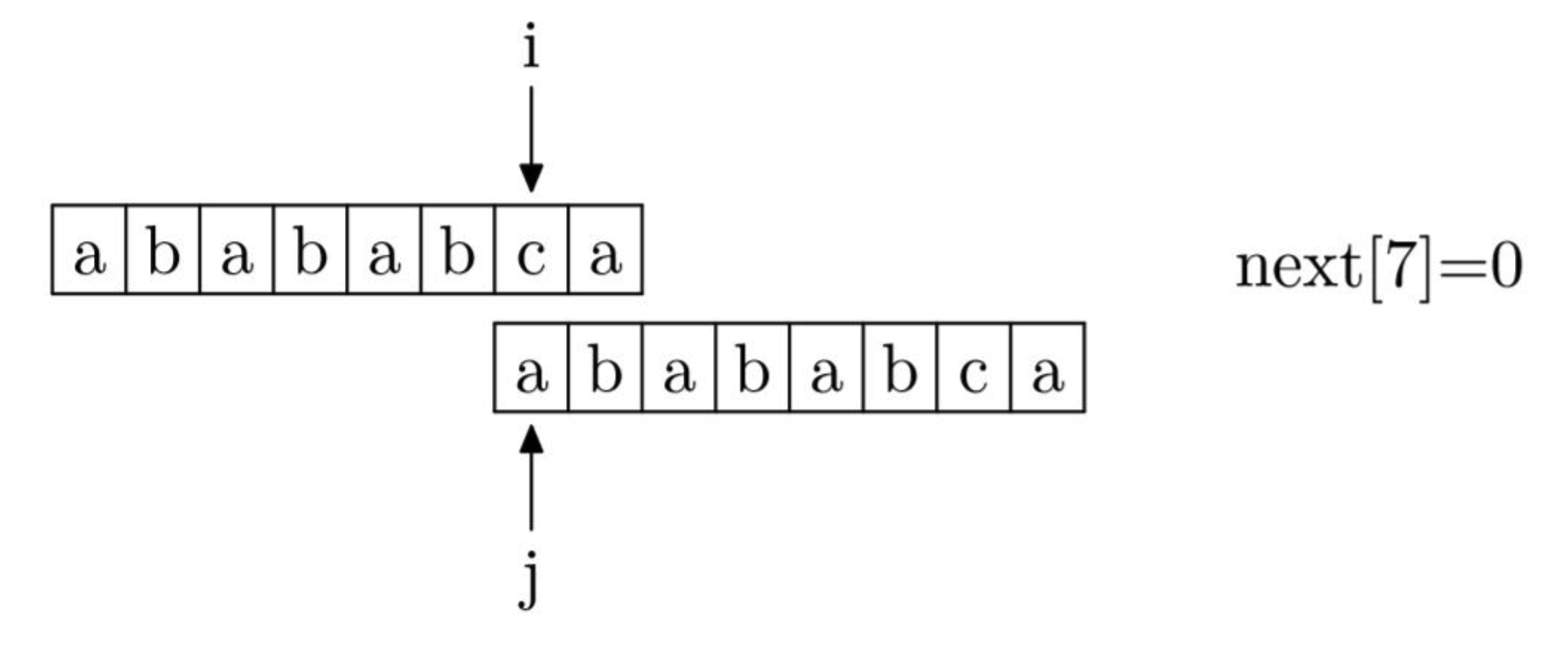
如果当前位置失配,则置 j=next[j],重复上述操作,直到匹配成功,或者 j=-1 (此时,next值为-1),如下图所示
细心的你会发现,上图中,next的下标与值与“主串当前位置的next值就是模式串当前位置的下标”这句话并对不上,这是为了编程的方便,实际应用的时候,将next数组数值全部+1,然后整体往左挪一位,最后将
next[0]置为-1即可。
这种方法的原理是什么呢?
假设上面例子中,已知 i=4 时的next值(即求 next[i+1]=next[5] ,或者说求 t=ababa 的最大公共元素长度)为3
在此基础上,求下一位的位置(即将i和j同时往右挪一位,即 i=5,j=3 )的next值( 即求 next[i+1]=next[6] ,或者说求 t=ababab 的最大公共元素长度)
通过前面的假设可知,t[i-3:i-1]=t[2:5]=aba 和t的前缀 t[0:3]=aba 是匹配成功的。
所以往后只需对 t[3] 和 t[5] 进行比较,如果比较成功,则说明 t[2:6] 和 t[0:4] 是匹配成功的(即两者为最大公共元素),即当前位置的next值为上一位置的next值+1(即 j+1);
否则,退而求其次,递归回溯到 j=next[j] (t[0:next[j]] 是 t[0:j] 的最大公共元素,即上一位置的最大公共元素的最大公共元素,特别地,t[0:next[j]] 是 t[0:i+1] 的公共元素),重复上述操作即可。
上面过程有个问题,如果回溯的过程中一直匹配失败怎么办?这引申出next数组的优化问题。
当 t[j]=t[next[j]] 时,如果回溯到 t[next[j]] 位置时,必然会再出现失配的情况。
首先,之所以会回溯到 t[next[j]],是因为与 t[j] 失配了。现在要与 t[next[j]] 进行匹配,但又因为 t[j]=t[next[j]] ,那当然还会导致失配。
那么,我们为什么不在保存next值的时候,加一层判断呢?当出现 t[j]=t[next[j]] 的时候,令 next[j]=next[next[j]] ,不断往前回溯,直到 t[j]!=t[next[j]] 为止,这样往后所有的回溯操作都只需要查一次next数组即可。
例如,字符串 abababca 未优化前的next数组为 [-1, 0, 0, 1, 2, 3, 4, 0],优化后的next数组为 [-1, 0, -1, 0, -1, 0, 4, -1]
2.2. 优缺点
KMP算法的预处理时间复杂度为 \(O(m)\),匹配时的时间复杂度为 \(O(n)\),总体时间复杂度为 \(O(m+n)\)。总体来说是比朴素的匹配算法的效率要高。
KMP算法尽管匹配效率已经优化了不少,但由于后面研究出了更为简单且优化效率更高的匹配算法,所以KMP算法使用到场景越来越少,已经成了昨日黄花了。
3. BM算法(Boyer-Moore Algorithm)
实现代码传送门
3.1. 基本思想
BM算法的特点是从模式串的末尾往前进行匹配,从而忽略主串中的部分字符,以减少遍历主串的代价。
对于每个字符匹配的结果,定义如下规则:如果字符失配,则将主串中该位置的字符称为 坏字符;如果字符匹配成功,则将模式串中该位置到末尾的序列称为 好后缀。
坏字符处理
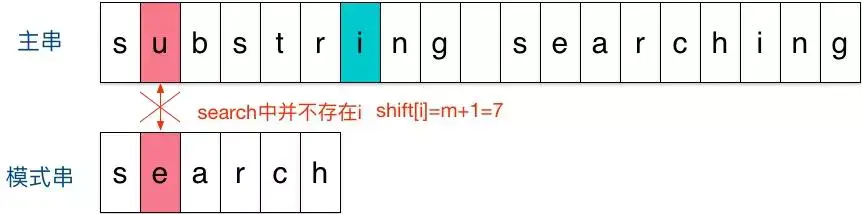
只要出现失配的情况,就一定会产生坏字符。例如,下图中的P就是坏字符
对此,只需要将模式串往右移动两位,使得坏字符与在模式串中最右出现的坏字符对齐,如下所示
上述 模式串移动的位数 = 当前模式串的位置 - 模式串当前位置的左边部分中坏字符最靠右出现的位置(即 \(2=6-4\) )。如果坏字符不包含在模式串之中,则最右出现位置为-1
从上面可以看出,这次移动过后,有2个字符直接被跳过不遍历了,只剩下4个字符有可能通过回溯被再次遍历。
好后缀处理
失配的时候,除了会出现坏字符,有时候也会出现好后缀。例如出现下图失配情况时, MPLE 就是一个好后缀
KMP算法中的公共元素和BM算法中的好后缀的区别:
公共元素是前缀和后缀相同的元素,而好后缀是主串和模式串相同的元素;
公共元素中的后缀是当前位置往前的后缀,好后缀中的后缀是当前位置往后的后缀。
特别地,MPLE、PLE、LE、E这些都是好后缀,但是只有E在模式串中出现了两次,故将模式串往右移动6位,将主串中的E和模式串中第一次出现的E对齐,如下图所示
上述 模式串移动的位数 = 当前模式串的位置 - 模式串当前位置的左边部分中好后缀最靠右出现的位置(即 \(6=6-0\) ),如果好后缀在模式串中没有再次出现,则为-1。
综上,比较两者启动的位数,择其大者移动模式串。
模式串移动后,继续从模式串的末尾往前重复匹配操作。
最后,由于这两个规则的移动位数只与匹配串有关,与主串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
3.2. 优缺点
一般情况下BM算法都会比KMP算法的效率高,所以,据说大部分编辑类软件查找功能使用的算法就是BM算法(未加考证)。
但个别情况下会出现相反的情况。例如,当主串为 baaaabaaaabaaaabaaaa,匹配串为 aaaaa 时,会处于最坏情况。
从上面可以看出,BM算法的时间复杂度是不稳定的。主串和匹配串的相似度越高,匹配串的信息熵越小,匹配时就越会趋向于最坏情况。事实上,实际的文本匹配中,出现最坏情况的概率较低,故匹配的平均时间复杂度趋近于最优情况时的时间复杂度。
匹配时最优情况的时间复杂度为 \(O(n/m)\),最坏情况为 \(O(nm)\)
4. Sunday算法
实现代码传送门
4.1. 基本思想
Sunday算法是BM算法的简化版,或者说是BM算法的升华版,其遍历主串的顺序为从前往后。
Sunday算法只保留了坏字符,抛弃了好后缀(事实上,由于好后缀处理起来比较麻烦,实际运用中,BM算法有时也会抛弃好后缀这一规则)
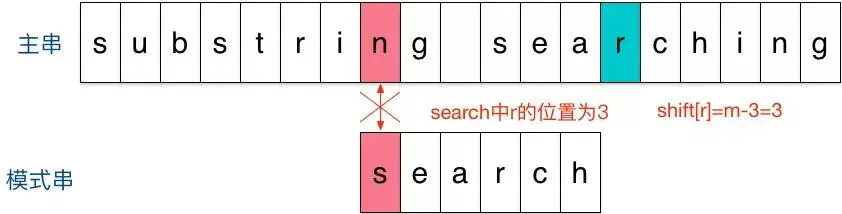
具体做法为,从左往右匹配主串和匹配串,当出现失配的情况时,则跳转到参与匹配的最末字符(并非正在匹配的)的下一位,将该字符当做坏字符,然后按BM算法的坏字符规则移动模式串即可,如下图所示
4.2. 优缺点
Sunday算法的优缺点和BM算法是一样,两者匹配时最优情况的时间复杂度都为 \(O(n/m)\),最坏情况都为 \(O(nm)\),但是Sunday算法比BM算法简单,据说平均性能Sunday算法会比BM算法好,但未进行验证。
Have fun~
5. references
http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
从头到尾彻底理解KMP(2014年8月22日版)_结构之法 算法之道-CSDN博客_kmp
http://www.voidcn.com/article/p-gcxakovf-sg.html
https://www.jianshu.com/p/a3f8d72c8405